圆周率 pi

#include<cmath>
M_PI; //圆周率pi

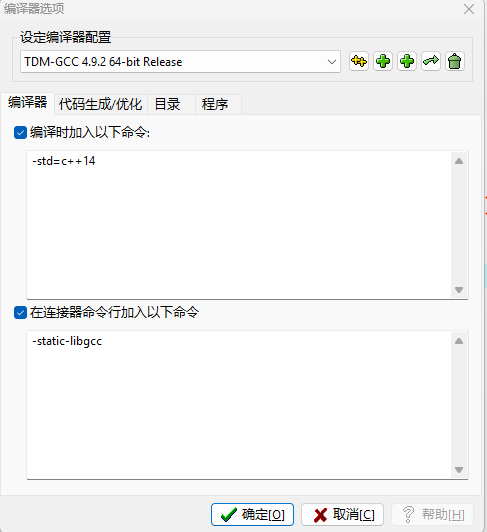
Dev-C++5.11设置编译选项：

菜单：工具->编译选项 在编译时加入-std=c++14; 在连接时加入-static-libgcc;

文件IO

freopen("题目英文名.in", "r", stdin);
freopen("题目英文名.out", "w", stdout);

程序的优化魔法（正式比赛时慎用）

#pragma GCC optimize("Ofast", "inline", "-ffast-math")
#pragma GCC target("avx,sse2,sse3,sse4,mmx")

notepad++加运行C++功能：

F5 -> 如下命令

cmd /k cd /d "$(CURRENT_DIRECTORY)" & g++ "$(FILE_NAME)" -o "$(NAME_PART)" & "$(NAME_PART).exe"

保存 -> "C/C++ compiler", 设置习惯的快捷键

关闭同步的cin，加快cin的速度

ios::sync_with_stdio(0);
cin.tie(0);
cout.tie(0); //endl -> '\n'

设置小数点位数：

//方法一：
#include<iomanip> 
cout << fixed << setprecision(2) << n << endl;
//方法二：
#include<cstdio>
printf("%.2lf\n", n);

int类型 的最大值和最小值

INT_MAX 等于2147483647 INT_MIN 等于-2147483648

快读

inline int read()
{
	int s = 0, f = 1;
	char c = ' ';
	for(; !(c >= '0' && c <= '9'); c = getchar()) 
		if(c == '-') f = -1;
	for(; c >= '0' && c <= '9'; c = getchar())
		s = (s << 1) + (s << 3) + (c ^ 48);
	return (f == -1) ? -s : s;
}

---

$2^n$2^n

$\le$\le

$\ge$\ge

$\geqslant$ \geqslant

$\leqslant$ \leqslant

$\sim$ \sim

$\times$ \times

$\cdot$ \cdot

$\div$ \div

$\pm$ \pm

$\mp$ \mp

$\neq$ \neq

$\approx$ \approx

$\equiv$ \equiv

$\in$ \in

$\Phi$ \Phi

$\lfloor a \rfloor$ \lfloor \rfloor

$O(N^{\frac{1}{2}})$
O(N^{\frac{1}{2}})

$\sqrt{log n ∙ log log n}$ \sqrt{log n ∙ log log n}

$n = \sum_{i=0}^{k}$ n = \sum_{i=0}^{k}

$n= \overline{abc}$ n= \overline{abc}

$$\sqrt {p(p−a)(p−b)(p−c)}$$

\sqrt {p(p−a)(p−b)(p−c)}

$$p=\frac{a+b+c}{2}$$

p=\frac{a+b+c}{2}

$$a^2+b^2_3+c^2$$

a^2+b^2_3+c^2

$$sum_{n=1}{n} = a_1+a_2+\dots+a_n$$

sum_{n=1}{n} = a_1+a_2+\dots+a_n

$$\lim_{n \to \infty} \sum_{k=1}^n \frac{1}{k^2} = \frac{\pi^2}{6} $$

\lim_{n \to \infty}
\sum_{k=1}^n \frac{1}{k^2}
= \frac{\pi^2}{6}

$$p^3_{ij} \qquad m_\mathrm{Knuth}\qquad \sum_{k=1}^3 k \\[5pt] a^x+y \neq a^{x+y}\qquad e^{x^2} \neq {e^x}^2 $$

p^3_{ij} \qquad
m_\mathrm{Knuth}\qquad
\sum_{k=1}^3 k 

\\[5pt]

a^x+y \neq a^{x+y}\qquad
e^{x^2} \neq {e^x}^2

$$f(x) = x^2 \quad f'(x) = 2x \quad f''^{2}(x) = 4$$

f(x) = x^2 \quad f'(x)
= 2x \quad f''^{2}(x) = 4

$$3/8 \qquad \frac{3}{8} \qquad \tfrac{3}{8}$$

3/8 \qquad \frac{3}{8}
\qquad \tfrac{3}{8}

$$\sqrt{x} \Leftrightarrow x^{1/2} \quad \sqrt[3]{2} \quad \sqrt{x^{2} + \sqrt{y}} $$

\sqrt{x} \Leftrightarrow x^{1/2} 

\quad \sqrt[3]{2}

\quad \sqrt{x^{2} + \sqrt{y}}

$LaTeX$数学符号大全

收藏夹：

kkksc03 的信息学竞赛百科目录